The Geometric Serie

The geometric series with ratio $r \in \mathbb{R}$ and constant $a$ is the following infinite sum:

$ar^0+ar^1+ar^2+\cdots +ar^n+\cdots$

This series converges if and only if $|r|<1$ , and its sum is:

$\sum_{n=0}^{\infty}ar^n=\lim_{n\to\infty}a\frac{1-r^{n+1}}{1-r}=\frac{a}{1-r}$

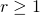If $r \ge 1$ , the series diverges.
If 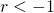$r<-1$ , the series oscillates between 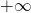$+\infty$ and $-\infty$ .
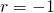If $r=-1$ , the series oscillates between 0 and $a$ .

Proof.

Let $s_n$ be the partial sum of the series $\sum_{n=0}^{\infty}ar^n$

Thus,

$s_n= \sum_{n=0}^{n}ar^n=a+ar+ar^2+\cdots+ar^n$

Multiplying $s_n$ by $r$ :

$r\cdot s_n= ra+ar^2+ar^2+\cdots+ar^{n+1}$

We observe that $r\cdot s_n$ contains all the terms of $s_n$ except for the first term $a$ and adds a new term, $ar^{n+1}$ .

That is, $r\cdot s_n= s_n -a+ar^{n+1}$ . We have obtained an equation for $s_n$ , so solving for $s_n$ :

$a-ar^{n+1}=s_n- r\cdot s_n \Rightarrow a(1-r^{n+1})=s_n(1-r) \Rightarrow s_n=\frac{ a(1-r^{n+1}) }{ (1-r) }$

As long as $r \neq 1$ , because otherwise, if $r=1$ , then $s_n$ would not be defined. We need a well-defined expression for $s_n$ to determine the sum for all values of $n$ , that is, $\forall n\in \mathbb{N}$ .

We have successfully expressed the $n$ terms of the sum in a general equation. This is very useful because the series is the limit of $s_n$ as $n\to\infty$ , and since we obtained an explicit expression for $s_n$ , we just need to compute this limit.

$\sum_{n=0}^{\infty}ar^n:= \lim_{n\to\infty} s_n=a\lim_{n\to\infty}\frac{1-r^{n+1}}{1-r}=a\lim_{n\to\infty}\frac{\frac{1}{r}-\frac{r^{n+1}}{r}}{\frac{1-r}{r}}= a\lim_{n\to\infty}\frac{\frac{1}{r}-r^n}{\frac{1-r}{r}}=$

$=a\frac{\frac{1}{r}- \lim_{n\to\infty} r^n}{\frac{1-r}{r}} \stackrel{|r|<1}{=} a\frac{\frac{1}{r}- 0}{\frac{1-r}{r}} =\frac{a}{1-r}$

As you can see, we used the restriction $|r|<1$ because otherwise, $\lim_{n\to\infty} r^n$ is not finite.

Reader Interactions