Is the Open Unit Disk an Open or Closed Set?

Exercise. Let $X$ = $\mathbb{R}^2$ be equipped with the Euclidean norm topology. Consider the set:

$A = \{(x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1\}$

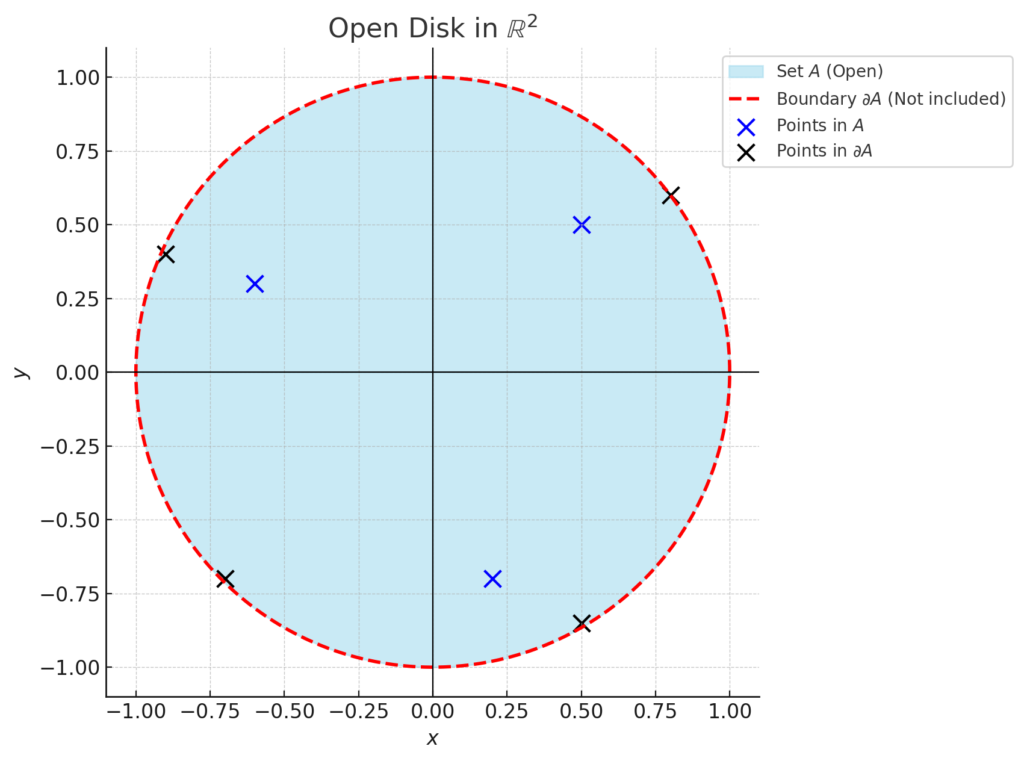
which represents the open unit disk in the plane. Determine whether $A$ is an open set, a closed set, or both.

The following is a very basic topology exercise that, despite its simplicity, provides an initial encounter with topological spaces—an essential concept even in the early stages of real analysis.

Step 1: Checking if A is Open

In $\mathbb{R}^2$ with the Euclidean topology, a set is open if for every point in the set, there exists an open ball around that point that is entirely contained within the set.

Let $p = (x_0, y_0)$ be any point in $A$ , meaning:

$x_0^2 + y_0^2 < 1.$

We define an open ball $B_r(p)$ centered at $p$ with radius $r$ :

$B_r(p) = \{(x,y) \in \mathbb{R}^2 \mid (x - x_0)^2 + (y - y_0)^2 < r^2 \}.$

Since $x_0^2 + y_0^2 < 1$ , we can always find a small enough $r$ so that $B_r(p) \subset A$ . This confirms that $A$ is an open set.

Step 2: Checking if A is Closed

A set is closed if it contains all its limit points, which means it contains its boundary.

The boundary of $A$ is the unit circle:

$\partial A = \{(x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1\}.$

However, this set is not included in $A$ , since $A$ consists only of points where $x^2 + y^2 < 1$ . Therefore, there exist limit points (points on the boundary) that are not in $A$ , meaning that $A$ is not closed.

Conclusion

The open unit disk $A$ is open in $\mathbb{R}^2$ with the Euclidean topology, but it is not closed because it does not contain its boundary points.

Step 1: Checking if A is Open

Step 2: Checking if A is Closed

Conclusion

Reader Interactions