Hallar los extremos relativos de una integral definida

Vamos a hallar los extremos relativos (si es que los hay) de la siguiente integral.

$F(x)=\int_{0}^{x^4}e^{sen(t^2-1)}dt$

Como veis, es una función que contiene una integral. Estamos asumiendo que es esta la integral de Riemann.

Necesitamos tener en mente el Teorema Fundamental del Cálculo. Que si lo recordamos nos dice:

Teorema. (Primer TFC)

Sea $f$ una función acotada e integrable en un intervalo $[a,b]$ con $a,b \in \mathbb{R}$ , $c \in [a,b]$ y $F$ la función definida en $[a,b]$ por
$F(x)= \int_{c}^{x}f(t)dt$

Si $f$ es continua en un punto $x\in[a,b]$ entonces $F$ es derivable en $x$ y $F'(x)=f(x)$ .

Así pues tenemos que verificar algunas propiedades de $F(x)$ y $f(t)$ para aplicar el Primer TFC.

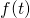$f(t)$ debe estar acotada en $[a,b]$ .

Sabemos que la función $sen(t)$ está acotada en $[-1,1]$ . Entonces $sen(t-1)$ también está acotada en $[-1,1]$ . Ahora debemos saber que ocurre al componerse con la función exponencial. Al tratarse $e^x,\;x\in[-1,1]$ de una función creciente bastará con evaluarla al valor mínimo y máximo de la función $sen(t^2-1)$ . Así pues el rango de $e^{sen(t^2-1)}$ estará entre $[\frac{1}{e},1]$ .

Hemos pues, comprobado que $f$ está acotada.

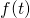$f(t)$ debe ser integrable en $[a,b]$

Esta propiedad la podemos verificar haciendo uso de este importante teorema:

Teorema. Si una función $f$ definida en $[a,b]$ es continua entonces es integrable.

Y vemos que $f(t)=e^{sen(t^2-1)}$ es una composición de funciones continuas, por lo tanto es continua, y por ende integrable.

Acabamos de ver que cumplimos las condiciones por hipótesis del Primer TFC. Estamos pues, en virtud de aplicarlo! 😀

Para usar esta importante ecuación parametrizamos un poco nuestras funciones. $g(x):=x^4$ y $h(x):=\int_{0}^{x}e^{sen(t^2-1)}dt$ . Así, expresamos $F(x)$ en función de $h$ y $g$ .

$F(x)=h(g(x))$

Aplicando la regla de la cadena:

$F'(x)=h'(g(x))\cdot g'(x)$

Por el 1er TFC $h'(x)=e^{sin(x^2-1)}$ , y $g'(x)=4x^3$ .

Finalmente

$F'(x)=e^{sin(x^8-1)}4x^3$

Hemos conseguido ya la derivada de $F'(x)$ , pasamos a la búsqueda de extremos relativos igualando a cero, $F'(x)=0$ .

$e^{sin(x^8-1)}$ es siempre mayor a cero, con lo cuál la igualdad se cumple únicamente para $x=0$ .

Usamos ahora la siguiente proposición.

Proposición. Sean $a \in \mathbb{R}$ y $f$ una función definida en un entorno de $a$ con derivada positiva en un intervalo a la izquierda de $a$ y negativa en un intervalo a la derecha de $a$ . Entonces $f$ tiene un máximo relativo en $a$ . Análogamente, si $f$ tiene derivada negativa en un intervalo a la izquierda de $a$ y derivada positiva en un intervalo a la derecha de $a$ entonces $f$ tiene un mínimo relativo en $a$ .

Con esta proposición deducimos de inmediato que tenemos un mínimo relativo en $x=0$ . Pues $F'(x)>0,\, \forall x>0$ y $F'(x)<0,\, \forall x<0$ .

Es el único extremo relativo? La respuesta es sí, y es gracias a que $F(x)$ es derivable en todo su dominio. De no ser así, el hecho que sólo $x=0$ , cumple $F'(x)=0$ no sería suficiente.

Esto viene de la siguiente proposición.

Proposición. Sea $f:A\subset \mathbb{R}\to\mathbb{R}$ derivable en $A$ . Si $f$ tiene un extremo relativo en $a$ entonces $f'(a)=0$ .

Y claro, la negación de la afirmación $f'(a)\neq 0$ implica que o bien $f$ no es derivable en $A$ o bien $a$ no es extremo relativo de $f$ y en efecto debe cumplirse la 2ª opción (no hay más extremos) pues la 1ª opción es falsa por hipótesis.

Reader Interactions