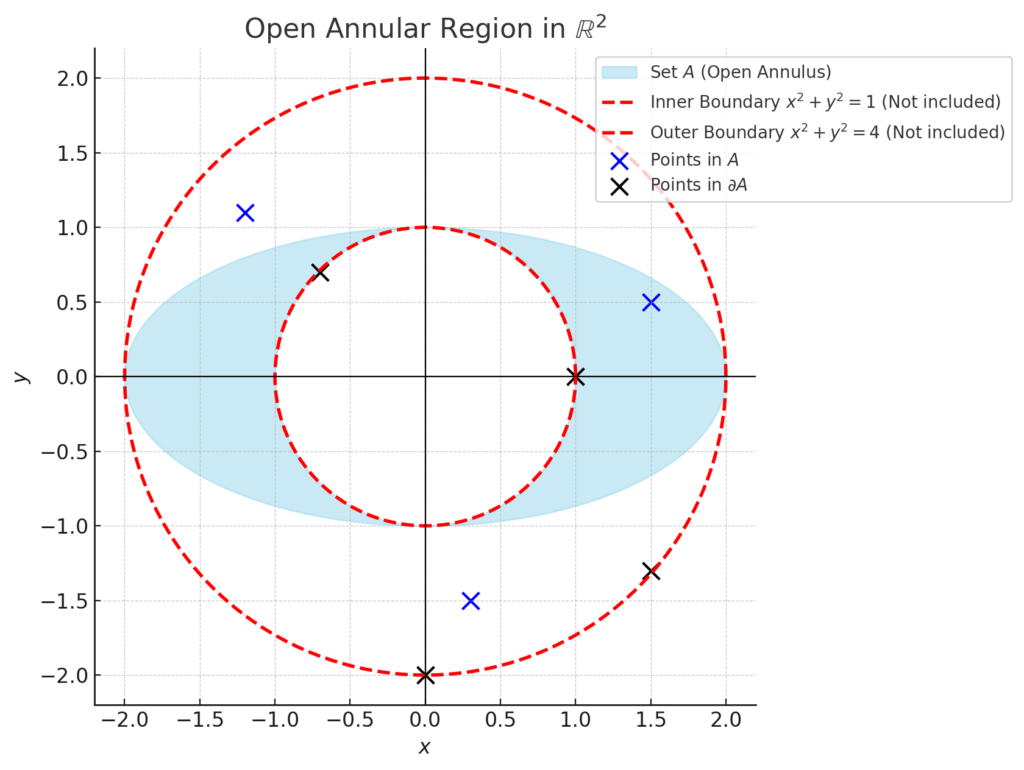
Let ![]() = ℝ² be endowed with the Euclidean topology. Consider the set:
= ℝ² be endowed with the Euclidean topology. Consider the set:
![]()
which represents an open annular region in the plane (the region between two concentric circles of radii 1 and 2, excluding the boundaries).
Question: Is the Open Annular Region an Open or Closed Set?
Step 1: Checking if A is Open
A set is open in the Euclidean topology if for every point in the set, there exists an open ball around that point that is entirely contained within the set.
Let ![]() be a point in
be a point in ![]() , meaning:
, meaning:
![]()
We define an open ball ![]() centered at
centered at ![]() with radius
with radius ![]() :
:
![]()
Since ![]() is strictly inside the annular region, we can always find a small enough
is strictly inside the annular region, we can always find a small enough ![]() such that
such that ![]() . This confirms that
. This confirms that ![]() is an open set.
is an open set.
Step 2: Checking if A is Closed
A set is closed if it contains all of its limit points, meaning it contains its boundary.
The boundary of ![]() is formed by the two circles:
is formed by the two circles:
![]()
These points are not included in ![]() , since
, since ![]() consists only of points where
consists only of points where ![]() . Therefore, there exist limit points (points on the boundary) that are not in
. Therefore, there exist limit points (points on the boundary) that are not in ![]() , meaning that
, meaning that ![]() is not closed.
is not closed.
Step 3: Finding the Boundary of A
The boundary of a set ![]() consists of all points where every open ball centered at them contains both points from
consists of all points where every open ball centered at them contains both points from ![]() and points from
and points from ![]() (the complement of
(the complement of ![]() ).
).
If we take a point on the inner circle ![]() , any open ball centered at that point will contain points from
, any open ball centered at that point will contain points from ![]() (where
(where ![]() ) and points from outside
) and points from outside ![]() (where
(where ![]() ). The same occurs for the outer circle
). The same occurs for the outer circle ![]() .
.
Thus, the boundary is:
![]()
Step 4: Modifying the Set
Now, consider a modified set ![]() defined as:
defined as:
![]()
How does this change the properties of the set?
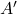 is no longer open because it includes its boundary, meaning points on the circles
is no longer open because it includes its boundary, meaning points on the circles 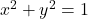 and
and 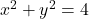 do not have open neighborhoods fully contained in
do not have open neighborhoods fully contained in 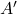 .
.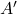 is now closed because it contains all of its limit points (the entire boundary is included).
is now closed because it contains all of its limit points (the entire boundary is included).
Conclusion
| Set | Open | Closed |
|---|---|---|
| ✅ Yes | ❌ No | |
| ❌ No | ✅ Yes |
This exercise illustrates how modifying a set by including or excluding its boundary affects its openness and closedness in the Euclidean topology.
