Determinar el carácter de una serie con una potencia en el numerador y una exponencial en el denominador

Vamos a mostrar algunos ejemplos donde veremos como determinar el carácter de una serie, es decir, ver si converge o por el contrario no converge (diverge).

Ejemplo 1. Calcular el carácter de la siguiente serie.

$\sum_{n=1}^{\infty}\frac{3^n}{2^n+n^2}$

Para calcular el carácter de la serie vamos a utilizar criterios de comparaciones. Los criterios de comparación se basan en el supuesto de si yo tengo una serie conocida es decir, se su carácter, entonces puedo obtener el carácter de mi serie de interés. Es por eso que nos será útil ver a qué serie conocida se parece nuestra serie.

Hay varios criterios de comparación, la idea es ver ejemplos de aplicación de cada uno de ellos, pero no nos preocupemos, con la práctica sabremos cuál de ellos nos conviene.

Ahí va uno que nos será útil para este ejemplo:

Proposición. (Criterio de comparación con paso al límite): Sean $(a_n)$ y $(b_n)$ dos sucesiones de números reale tales que $a_n\ge 0$ y $b_n>0$ para todo $n \in \mathbb{N}$ suponiendo que

$\lim_{n}\frac{a_n}{b_n}=l\in\mathbb{R}$

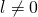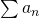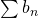Si $l\neq0$ , entonces las dos series $\sum a_n$ y $\sum b_n$ tienen el mismo carácter-.
Si 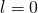$l=0$ y la serie 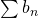$\sum b_n$ es convergente, entonces la serie 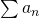$\sum a_n$ también es convergente.

Muy bien. Ahora tenemos que coger una serie de referencia, según la nomenclatura de la proposición anterior nuestra series es $\sum_{n=1}^{\infty} a_n = \sum_{n=1}^{\infty} \frac{3^n}{2^n+n^2}$ . Vamos a hallar una serie $\sum_{n=1}^{\infty}b_n$ que sepamos su carácter ya que según la proposición anterior nos dice que si sabemos el carácter de $\sum_{n=1}^{\infty}b_n$ y el límite es $l\neq0$ o $l=0$ entonces automáticamente sabemos el carácter de $\sum_{n=1}^{\infty} a_n$ .

Así pues la serie de $\sum_{n=1}^{\infty}b_n$ a elegir puede ser:

$\sum_{n=1}^{\infty}\frac{3^n}{2^n}= \sum_{n=1}^{\infty}\left ( \frac{3}{2} \right )^n$

y esta es una serie geométrica. Recordemos que una serie geométrica es del tipo $\sum_{n=0}^{\infty}ar^n$ y es una serie convergente si la razón $r$ en valor absoluto es menor a uno, es decir, $\left | r \right |<1$ . Y en particular su suma es $\frac{a}{1-r}$ . Podéis ver la demostración en este enlace. https://tenzorial.com/?p=171&preview=true

Para nuestro caso $r=\frac{3}{2}$ y $a=1$ . Como esta serie de referencia nos sirve para comparar podríamos elegir otra serie geométrica, pero como vamos a utilizar el ‘Criterio de comparación con paso al límite’ nos interesa que el límite del cociente de la sucesión de nuestra serie $a_n= \frac{3^n}{2^n+n^2}$ entre la sucesión de referencia $b_n= \left ( \frac{3}{2} \right )^n$ sea un número real. Tal y como indica en la proposición, $l \in \mathbb{R}$ .

Así pues el criterio de la serie geométrica consiste en ver en que intervalo pertenece $r$ , si $|r|<1$ la serie geométrica converge y su $r\ge1$ la serie diverge.

Para nuestro caso $\sum_{n=1}^{\infty}\frac{3^n}{2^n}$ Como la razón $r=\frac{3}{2}\ge 1$ esta serie diverge.

Ahora ya tenemos una sucesión de referencia para comparar con la sucesión de nuestra serie. Comparemos-las por medio del criterio que hemos anunciado de comparación con paso al límite.

Es decir, tenemos que calcular el límite cuando $n$ tiende a infinito del cociente de sucesiones. Nuestra sucesión de interés es $a_n= \frac{3^n}{2^n+n^2}$ .

Entonces tenemos que:

$\lim_{n} \frac{a_n}{b_n}=\lim_{n}\frac{ \frac{3^n}{2^n+n^2}}{\left ( \frac{3}{2} \right )^n}=\lim_{n}\frac{3^n2^n}{3^n(2^n+n^2)}=\lim_{n}\frac{2^n}{2^n+n^2} = \lim_{n}\left ( \frac{2^n}{2^n+n^2} \right )\frac{\frac{1}{ 2^n }}{\frac{1}{ 2^n } }=$

$= \lim_{n}\frac{\frac{2^n}{ 2^n }}{\frac{2^n+n^2}{ 2^n }} = \lim_{n}\frac{\frac{2^n}{ 2^n }}{\frac{2^n}{ 2^n }+\frac{n^2}{ 2^n }} = \lim_{n}\frac{1}{1+\frac{n^2}{ 2^n }} =$

$= \frac{1}{1+\lim_{n}\frac{n^2}{ 2^n }}$

Para resolver este límite vamos a hacer uso de un teorema. Antes de hacerlo comentar que bastante frecuente resolver este límite de forma más informal argumentando que en el denominador hay una una función exponencial y esta crece mucho más rápidamente que una función potencial que es la que encontramos en el numerador. Y por tanto un denominador que cada vez es más grande que su numerador hace que ese cociente este cada vez más cercano a cero. Podemos ver seguidamente como $2^n$ crece con mucha más velocidad que $n^2$ .

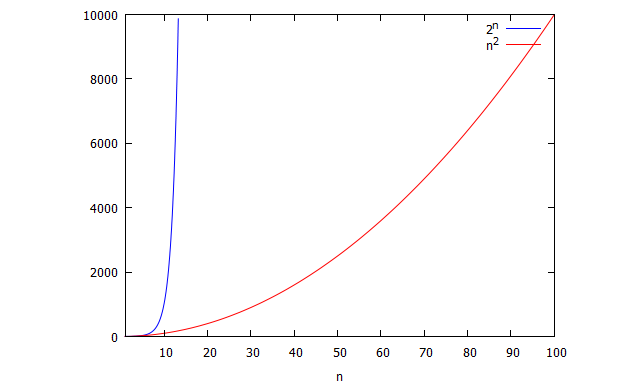
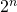Observamos como la función exponencial $2^n$ crece con mucha más velocidad que la función potencial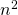 $n^2$

¡Aunque no nos perdamos de vista!, hemos discutido visualmente e intuitivamente el valor del límite $\lim_{n}\frac{n^2}{ 2^n }$ pero vayamos a lo interesante, es decir, a demostrar matemáticamente su valor.

Para ello haremos uso de el siguiente teorema, sencillito pero potente.

Teorema. Sea $x_n$ una sucesión de números reales positivos tales que existe el siguiente límite $L:=\lim_{n} \frac{x_{n+1}}{x_{n}}$ . Si $L<1\Rightarrow \lim_{n} x_n =0$ .

Apliquemos pues este teorema calculando $L$ para nuestro caso. Para nosotros la sucesión $x_n$ de interés es $\frac{n^2}{ 2^n }$ .

$\lim_{n} \frac{(n+1)^2}{2^{n+1}}\div\frac{n^2}{2^n}= \lim_{n} \frac{(n+1) 2^n }{n^2 2^{n+1}}= \lim_{n} \frac{(n+1)^2}{2n^2}= \lim_{n} \frac{n^2+2n+1}{2n^2}=$

$= \lim_{n} \frac{\frac{ n^2 }{ n^2 }+\frac{ 2n }{n^2}+\frac{1}{n^2 }}{\frac{ 2n^2 }{n^2}}= \frac{1+ \lim_{n} \frac{ 2n }{n^2}+ \lim_{n} \frac{1}{n^2 } }{ \lim_{n} \frac{ 2n^2 }{n^2} }=\frac{1+0+0}{2}=\frac{1}{2}$

Vemos que $L=\frac{1}{2} <1$ por tanto el límite $\lim_{n} \frac{(n+1)^2}{2^{n+1}}=0$ como queríamos demostrar.

Así pues ya podemos obtener el límite del cociente de sucesiones $a_n$ y $b_n$ .

$l:= \lim_{n}\frac{a_n}{b_n} =\lim_{n}\frac{ \frac{3^n}{2^n+n^2}}{\left ( \frac{3}{2} \right )^n} = \frac{1}{1+\lim_{n}\frac{n^2}{ 2^n }} = \frac{1}{1+0}=1$

Por el Criterio de comparación con paso al límite $l=1\neq 0$ esto implica que $\sum a_n$ y $\sum b_n$ tienen el mismo carácter. Y como $b_n$ era divergente por el criterio de la serie geométrica, $\sum a_n$ es también divergente.

Ejemplo 1. Calcular el carácter de la siguiente serie.

Reader Interactions