Calcular el desarrollo de Taylor y dominio de convergencia de una función de variable compleja

Dada una función de variable compleja $f: \mathbb{C} \to \mathbb{C}$ definida como $f(z)=\frac{1}{z+1}$ nos piden: hallar su desarrollo de Taylor en torno al punto $z=1$ y su respectivo dominio de convergencia.

Recordemos que el polinomio de Taylor para el caso real toma la expresión:

$\sum_{n=0}^{\infty}\frac{f^{n}(a)}{n!}(\textcolor{blue}{x}-a)^n$

Es una serie (suma infinita), con derivadas n-ésimas, como va al infinito deberá ser $f$ infinitamente diferenciable para que esté bien definida la serie.

Para el caso complejo, utilizamos la misma definición pero pasándola al “mundo” complejo. Es decir, el polinomio de Taylor para una función de variable compleja será: $f(z)=\sum_{n=0}^{\infty}\frac{f^{n}(a)}{n!}(\textcolor{blue}{z}-a)^n$ . Como podeis ver, es exactamente la misma definición lo único que la función involucrada es de variable compleja. (Recordemos la convención de denotar la variable $z$ cuando trabajamos con funciones complejas, y como $x$ para variables de funciones reales).

Primero de todo debemos comprobar si nuestra función es infinitamente derivable. Es por eso que es fundamental conocer el siguiente teorema.

Teorema. Sea $f : A \to \mathbb{C}$ una función holomorfa, $A \subset \mathbb{C}$ abierto, y $a \in A$ , entonces existe la derivada de orden $n$ en $a$ para todo $n\in\mathbb{N}$ .

Este teorema es una consecuencia del teorema de Taylor (para funciones complejas), queda no obstante fuera del propósito del ejercicio ver dicho teorema, lo importante ahora es quedarnos con este potente resultado.

Por tanto debemos comprobar si $f(z)=\frac{1}{1+z}$ es holomorfa (o derivable en sentido complejo) para demostrar la existencia de su desarrollo de Taylor. Obviamente no está definida en $z=-1$ puesto que se anula el denominador. El dominio de $f$ es por tanto $\mathbb{C}\setminus \left{1 \right}$ .

$\displaystyle \lim_{h \to 0}\frac{f(z+h)-f(z)}{h}=\lim_{h \to 0}\frac{\frac{1}{z+h+1}-\frac{1}{z+1}}{h}=$

$=\lim_{h \to 0}\frac{\frac{z+1-(z+1+h)}{(z+1+h)(z+1)}}{h}=\lim_{h \to 0}\frac{\frac{-h}{(z+1+h)(z+1)}}{h}=\lim_{h \to 0}\frac{-h}{h(z+1+h)(z+1)} =$

$=\frac{1}{z+1}\lim_{h \to 0}\frac{-h}{h(z+1+h)} = \frac{1}{z+1}\lim_{h \to 0}\frac{-1}{z+1+h} = \frac{1}{z+1}\frac{-1}{z+1} = \frac{-1}{(z+1)^2}$

Como vemos existe la derivada compleja (puesto que el límite ha convergido), luego (por el teorema previo) existirán sus respectivas derivadas de orden superior.

Ahora debemos obtener una expresión genérica para las derivadas enésimas de $f$ . Puesto que la serie de Taylor incorpora el término $f^{(n)}$ .

La mejor manera de hallarla es empezar calculando sus primeras derivadas iteradas. Usaremos la regla derivada para $(z^n)'=n\cdot z^{n-1}$ .

$f^{(0)}(z) := f(z) = (1+z)^{-1}$

$f^{(1)}(z) = -(1+z)^{-2}$

$f^{(2)}(z) = 2(1+z)^{-3}$

$f^{(3)}(z) = -6(1+z)^{-4}$

$f^{(4)}(z) = 24(1+z)^{-5}$

$\vdots$

$\textcolor{blue}{f^{(n)}(z) = n!(1+z)^{-n-1}(-1)^n}$

El término $(-1)^n$ lo ponemos porque como se ve, las derivadas de orden par son positivas y las de orden impar negativas, así conseguimos una expresión que generaliza cualquier caso (orden par o impar).

Al encontrar $f^{(n)}$ tenemos el ingrediente necesario para conocer el desarrollo de Taylor para $f$ , con $a=1$ . Ahora vamos a simplificar la expresión del desarrollo con tal de poder hallar el radio o dominio de convergencia.

$\sum_{n=0}^{\infty}\frac{\textcolor{blue}{f^{(n)}(a)}}{n!}{(z-a)^n = \sum_{n=0}^{\infty}\frac{f^{(n)}(1)}{n!}{(z-1)^n =$

$= \sum_{n=0}^{\infty}\frac{\textcolor{blue}{n!(1+1)^{-n-1}(-1)^n}}{n!}(z-1)^n=\sum_{n=0}^{\infty}\frac{n!\left (\frac{1}{2} \right )^{n+1}(-1)^n}{n!}(z-1)^n=\frac{1}{2}\sum_{n=0}^{\infty}\left (\frac{1-z}{2} \right )^n$

Observamos que esta es una serie geométrica de razón $\frac{1-z}{2}$ . Para que la serie sea convergente deberá cumplirse que $\left|\frac{1-z}{2} \right|<1$ . De esta desigualdad deducimos que $|1-z|<2$ .

Tomando $z=x+iy$ ,

$|1-z|<2\Leftrightarrow |1-x-iy|<2 \Leftrightarrow\sqrt{(1-x)^2+(-y)^2}<2\Leftrightarrow$

$\Leftrightarrow (1-x)^2+(-y)^2 < 2^2\Leftrightarrow (x-1)^2+y^2<2^2$

Y dado que la ecuación de una circunferencia en el plano es de la forma $(x-a)^2+(y-b)^2=r^2$ , tendremos una circunferencia en el plano complejo, con centro $(a=1,b=0)$ y radio $r=2$ .

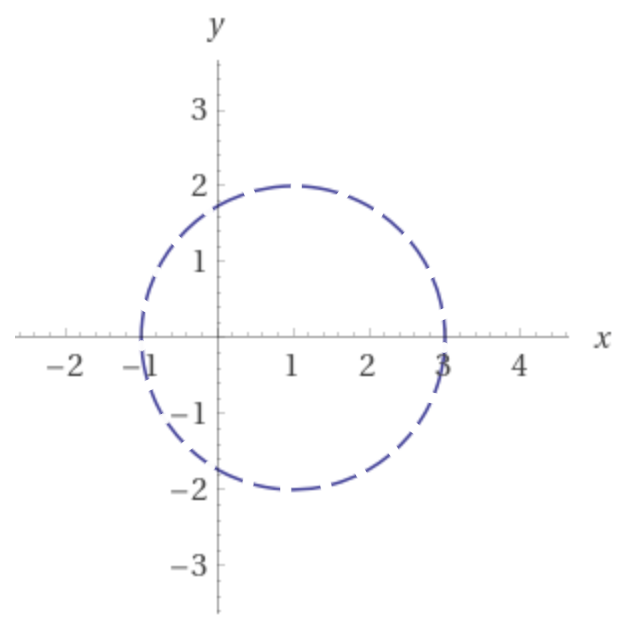
Como no tenemos una igualdad sino una desigualdad estrictamente menor ( $<$ ) el dominio de convergencia no incluye a la circunferencia (o borde de la bola) sino a su interior. En otras palabras, la región de convergencia puede verse como la bola abierta de centro $(1,0)$ y radio $2$ , puede denotarse de manera más compacta como $B_{2}((1,0))$ .

Reader Interactions