The geometric series with ratio ![]() and constant
and constant ![]() is the following infinite sum:
is the following infinite sum:
![]()
This series converges if and only if ![]() , and its sum is:
, and its sum is:
![]()
- If
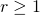 , the series diverges.
, the series diverges. - If
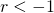 , the series oscillates between
, the series oscillates between 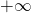 and
and  .
. - If
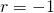 , the series oscillates between 0 and
, the series oscillates between 0 and  .
.
Proof.
Let ![]() be the partial sum of the series
be the partial sum of the series ![]()
Thus,
![]()
Multiplying ![]() by
by ![]() :
:
![]()
We observe that ![]() contains all the terms of
contains all the terms of ![]() except for the first term
except for the first term ![]() and adds a new term,
and adds a new term, ![]() .
.
That is, ![]() . We have obtained an equation for
. We have obtained an equation for ![]() , so solving for
, so solving for ![]() :
:
![]()
As long as ![]() , because otherwise, if
, because otherwise, if ![]() , then
, then ![]() would not be defined. We need a well-defined expression for
would not be defined. We need a well-defined expression for ![]() to determine the sum for all values of
to determine the sum for all values of ![]() , that is,
, that is, ![]() .
.
We have successfully expressed the ![]() terms of the sum in a general equation. This is very useful because the series is the limit of
terms of the sum in a general equation. This is very useful because the series is the limit of ![]() as
as ![]() , and since we obtained an explicit expression for
, and since we obtained an explicit expression for ![]() , we just need to compute this limit.
, we just need to compute this limit.
![Rendered by QuickLaTeX.com \[ \sum_{n=0}^{\infty}ar^n:= \lim_{n\to\infty} s_n=a\lim_{n\to\infty}\frac{1-r^{n+1}}{1-r}=a\lim_{n\to\infty}\frac{\frac{1}{r}-\frac{r^{n+1}}{r}}{\frac{1-r}{r}}= a\lim_{n\to\infty}\frac{\frac{1}{r}-r^n}{\frac{1-r}{r}}= \]](https://tenzorial.com/wp-content/ql-cache/quicklatex.com-f7788b52879ae6d5098912a505ebf467_l3.png)
![]()
As you can see, we used the restriction ![]() because otherwise,
because otherwise, ![]() is not finite.
is not finite.
